中国古代数学成就非常突出,中国人很早就掌握了数的概念,并且采用了十进位制,这是最先进、最科学的记数法。李约瑟说:“如果没有这种十进位制,就不可能出现我们现在这个统一化的世界了。”殷商时已经有了四则运算,春秋战国时正整数乘法口诀“九九歌”已经形成,此后“九九歌”成为普及数学知识的基础之一,一直延续至今。
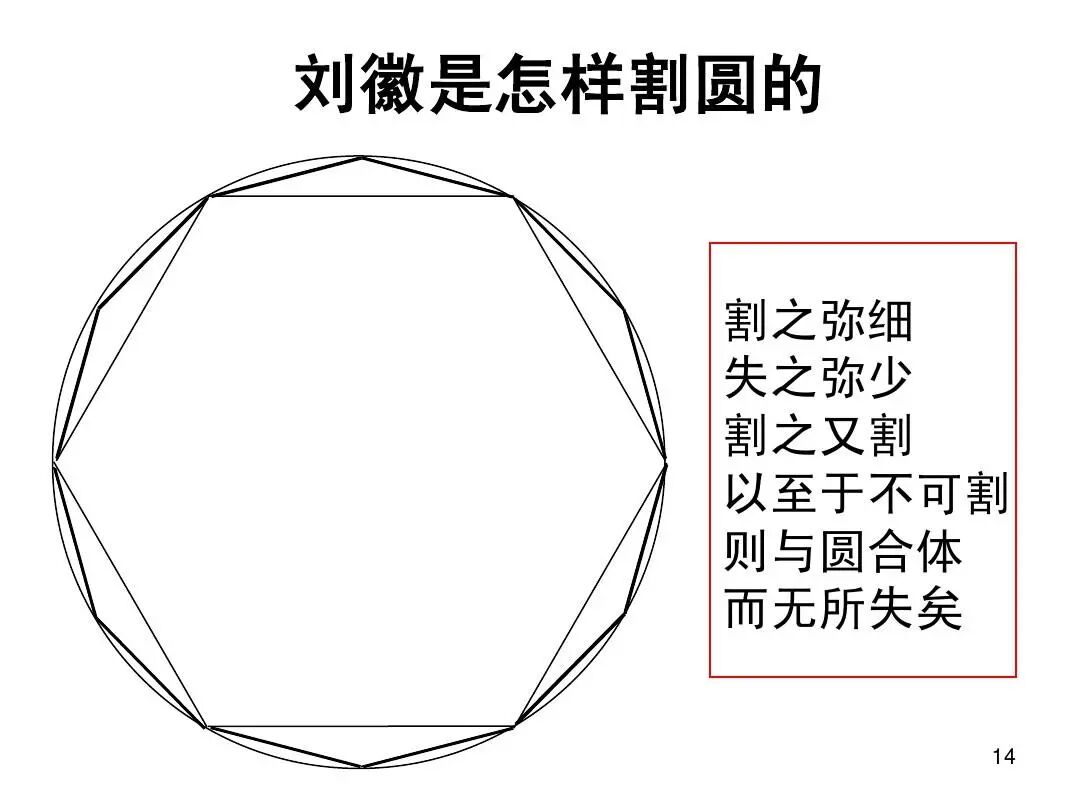
三国时期,刘徽运用割圆术求圆周长度,他认为无限增加圆内接正多边形的边数,其周长则愈接近圆周长,“割之弥细,所求弥小”,他运用这种方法,求得圆周率π=3927/1250。后来,祖冲之又将圆周率进一步精确到3.1415926到3.1415927之间。
隋代刘焯创立了等间距二次内插法,唐代僧一行创立了不等间距二次内插法,王孝通得到求解三次方程的方法,宋元时期得到关于高次方程组的求解法、一次同余式解法等。这些成果都处于当时的领先地位。
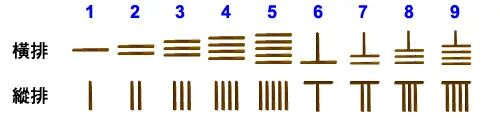
在计算工具方面,殷商时发明了“算筹”,算筹是圆形小竹棍,后来又有了骨制、铁制的。以算筹表示数目,有纵、横两种形式。以算筹为工具进行的计算叫“筹算”,计算时纵式表示个位、百位……横位表示十位、千位……遇零则空一个位置。
算盘产生于唐宋时期,形状为长方形,四周有框,内有直柱,中横为梁。梁上二珠,每珠作数5,梁下五珠,每珠作数1。算盘一般为9档到15档,运算时先定位再拨珠计算。明清两代,算盘成为当时工商贸易中不可缺少的工具。算盘携带方便,运算准确迅速,在相当长的一段时间内发挥着巨大作用。
伴随着数学知识的丰富和研究的深入,我国古代出现了许多有关数学研究的著作。这些书籍记录了历代数学成就。中国古代的许多数学家曾经写下了不少著名的数学著作,许多具有世界意义的成就正是因为有了这些古算书而得以流传下来,这些算书是我们了解中国古代数学成就的丰富宝库。
隋唐时期,国子监算学科将秦汉至唐朝一千多年间的十部著名数学著作作为算学教科书,分别是《周髀算经》《九章算术》《海岛算经》《五曹算经》《孙子算经》《夏侯阳算经》《张丘建算经》《五经算术》《缉古算经》《缀术》,数学教育和考试也会参考这十部著作,后世通称为《算经十书》,其中大多数还曾传入朝鲜和日本,成为他们进行数学教育和考试的教科书。《算经十书》是我国古代具有代表性的数学典籍,内容丰富、研究深入,在我国古代数学领域具有重要地位,对建立中国古代数学教育制度至关重要,是了解我国古代数学的重要著作。
《周髀算经》是我国最早的一部算学著作。《周髀算经》原名《周髀》,算经的十书之一,是中国最古老的天文学和数学著作,约成书于公元前1世纪,主要阐明当时的盖天说和四分历法。唐初规定它为国子监明算科的教材之一,故改名《周髀算经》。此书总结了春秋战国时代的数学成就,其中的勾股术“折矩以为勾广三,股修四,径隅五”,比古希腊毕达哥拉斯定理的发现早了500多年。
《九章算术》大约成书于公元1世纪中叶,对秦汉数学成就作了全面的反映。全书以问题集的形式,收录了246个应用题,共分为九章,即方田、粟米、衰分、少广、商功、均输、盈不足、方程和勾股。此书既注重理论,更注重实际问题的解决,这种思想对后代数学研究产生了重大影响。其影响之深,以致后来中国数学著作大体采取两种形式:或为之作注,或仿其体例著书。甚至西算传入中国之后,人们著书立说时还常常把包括西算在内的数学知识纳入九章的框架。但《九章算术》亦有其不容忽视的缺点:没有任何数学概念的定义,也没有给出任何推导和证明。魏景元四年(263年),刘徽给《九章算术》作注,才大大弥补了这个缺陷。
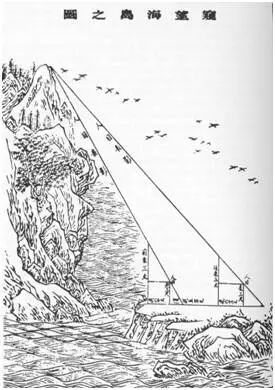
《海岛算经》略称《海岛》,是中国古代测量数学专著,魏晋时期的数学家刘徽所著。他在为《九章算术》作注时,写了《重差》一卷,附于该书中《勾股》章之后。唐代初年数学家李淳风将《重差》单列出来,取名《海岛算经》,并将其列为国子监算学诸生必读的“十部算经”之一,与李淳风注文一并传世。通行本有:清《四库全书》本、《微波榭算经十书》本、《武英殿聚珍版丛书》本、近代《丛书集成》本、一九六三年中华书局版钱宝琮校点《算经十书》本等。该书全部9个算例,均涉及测高望远及其计算问题。这是借助矩、表、绳的简单测量工具,依据相似直角三角形对应边成比例的内在关系,进行测高、望远、量深的理论和方法。
《孙子算经》是中国古代重要的数学著作,成书大约在四、五世纪,作者生平和编写年份不详。传本的《孙子算经》共三卷。卷上叙述算筹记数的纵横相间制度和筹算乘除法,卷中举例说明筹算分数算法和筹算开平方法。卷下第31题,可谓是后世“鸡兔同笼”题的始祖,后来传到日本,变成“鹤龟算”。
《张丘建算经》约成书于公元5世纪,现传本有92问。其比较突出的成就有最大公约数与最小公倍数的计算、各种等差数列问题的解决、某些不定方程问题的求解等。“百鸡问题”是《张丘建算经》中的一个著名数学问题,它给出了由三个未知量的两个方程组成的不定方程组的解。百鸡问题是:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。凡百钱买鸡百只,问鸡翁母雏各几何。”
《五经算术》是北周甄鸾所著,共二卷。书中对《易经》《诗经》《尚书》《周礼》《仪礼》《礼记》《论语》《左传》等儒家经典及其古注中与数字有关的地方详加注释,对研究经学的人或可有一定的帮助,但就数学的内容而论,其价值有限。现传本亦系抄自《永乐大典》。
《五曹算经》是算经十书之一,古代中国数学著作。一般认为由北周甄鸾所作,李淳风等为之作注。甄鸾通历法,曾编《天和历》,于566年颁行。“五曹”是指五类官员。其中“田曹”所收的问题是各种田亩面积的计算,“兵曹”是关于军队配置、给养运输等的军事数学问题,“集曹”是贸易交换问题,“仓曹”是粮食税收和仓窖体积问题,“金曹”是丝织物交易等问题。全书共收67个问题,其数学内容没有超出《九章算术》的内容。其南宋刻本,收藏于北京大学图书馆。
《缉古算术》又名《缉古算经》,也省称《缉古》,是唐代王孝通编著的一部数学著作,是我国古代著名的《算经十书》之一。其书大旨以补《九章算术·商功篇》之不足,故名《缉古算术》。该书根据汉以来有关二次方程及其解法的成就,论述解三次方程的问题。共收二十题,除第一题涉及到历法外,其余题目都是体积计算和勾股定理的运用,大多题的解法用到三次方程,解决了土建水利工程中出现的大量实际问题。这比西方提出解三次方程的方法要早六百多年。
《夏侯阳算经》是晋代夏侯阳所撰的数学著作。北宋元丰九年(1084年)所刻《夏侯阳算经》是唐中叶的一部算书。引用当时流传的乘除捷法,解答日常生活中的应用问题,保存了很多数学史料。原书已失传无考。
《缀术》是中国南北朝时期的一部算经,汇集了祖冲之和祖暅之父子的数学研究成果。《缀术》是祖冲之所作,还是祖暅之所作,中国数学史界至今没有定论。这本书被认为内容深奥,以致“学官莫能究其深奥,故废而不理”(《隋书》)。《缀术》在唐代被收入《算经十书》,成为唐代国子监算学课本,当时学习《缀术》需要四年的时间,可见《缀术》的艰深。《缀术》曾经传至朝鲜、日本,但到北宋时这部书就已亡佚。
宋元时期,中国古代数学发展到了鼎盛阶段,在这个时期很多数学家都为古代数学的发展作出贡献,其中秦九韶、李冶、杨辉和朱世杰成就最为突出,被誉为“宋元数学四大家”。
宋元算书主要以这四位数学家的著作为代表,包括:秦九韶著的《数书九章》,杨辉的《杨辉算法》,李冶的《测圆海镜》和《益古演段》,朱世杰的《算学启蒙》和《四元玉鉴》等。
《数书九章》是南宋数学家秦九韶所著数学著作。书中共列算题81问,分为9类。全书采用问题集的形式,并不按数学方法来分类。题文也不只谈数学,还涉及自然现象和社会生活,成为了解当时社会政治和经济生活的重要参考文献。该书在数学内容上颇多创新,是对《九章算术》的继承和发展。它概括了宋元时期数学的主要成就,标志着中国古代数学的高峰。
《杨辉算法》是宋代数学家杨辉的三种后期六卷数学著作的总称,这三种著作是《乘除通变算宝》卷上下、《田亩比类乘除捷法》卷上中下、和《续古摘奇算法》。
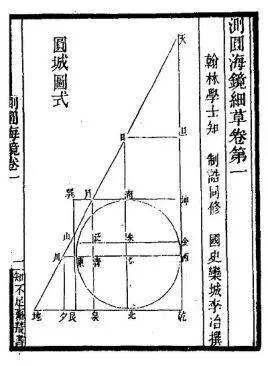
《测圆海镜》是元代李冶所著中国古代数学著作。成书于1248年,全书共有12卷,170问。这是中国古代论述容圆的一部专著,也是天元术的代表作。在《测圆海镜》问世之前,我国虽有文字代表未知数用以布列方程和多项式的工作,但是没有留下系统的记载。李冶在《测圆海镜》中系统而概括地总结了天元术,使文词代数开始演变成符号代数。
《益古演段》由李冶撰写,成书于1259年,全书共64问。“益古”指蒋周的《益古集》,“演段”指蒋周的算书。书中天元术、条段法二术并列,并且揭示两者的区别与联系。《益古演段》把天元术用于解决实际问题,研究对象是日常所见的方、圆的面积,所求多为圆径、方边、周长之类,内容安排基本上是从易到难。此书在进一步普及天元术的基础上进行一定的理论创新。
《算学启蒙》是一部通俗数学名著,上中下三卷,元大德己亥(1299年)朱世杰撰,共20门,凡259问。这部书从乘除运算讲到天元术,介绍了当时数学所包含的各方面内容,由浅入深,循序渐进,自成系统,内容深入浅出,通俗易懂,是一部重要的数学启蒙读物。本书原始版本,今已失传。现存版本中,最早的当推日本筑波大学所藏15世纪朝鲜李世宗时期的铜活字本。
《四元玉鉴》是我国宋元数学的又一个标志性著作,由元代朱世杰撰写,分卷首、上卷、中卷、下卷,24门,收录288问,成书于大德七年(1303年),介绍了朱世杰在多元高次方程组的解法——四元术,以及高阶等差级数的计算——垛积术、招差术等方面的研究和成果。此书代表着宋元数学的最高水平,美国科学史家萨顿称赞它“是中国数学著作中最重要的一部,同时也是中世纪的杰出数学著作之一”。
《九章算法比类大全》是明代吴敬撰写的算书,亦名《九章详注比类算法大全》。明代前期的算书,十卷首一卷,成书于1450年。该书卷首为“乘除开方起例”,旨在讲解算法的基本理论,列举了大数记法、小数记法、度量衡制单位、整数分数四则运算、定位、开方、差分等项,并用诗歌形式一一作了解释。卷首还提出一种以前中国数学著作中未曾出现过的“写算法”。
《算法统宗》全称《新编直指算法统宗》,是中国古代数学名著,明代数学家程大位著。《算法统宗》共17卷,卷1、卷2介绍数学名词、大数、小数和度量衡单位以及珠算盘式图、珠算各种算法口诀等,并举例说明具体用法;卷3至卷12按“九章”次序列举各种应用题及解法;卷13到卷16为“难题”解法汇编;卷17“杂法”,为不能归入前面各类的算法,并列有14个纵横图。书后附录“算经源流”一篇,著录了北宋元丰七年(1084年)以来的数字书目51种。万历二十一年(1593年)刊行。
《算法统宗》是一部应用数学书,是以珠算为主要的计算工具,列有595个应用题的数字计算,都不用筹算方法,而是用珠算演算。评述了珠算规则,完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变。《算法统宗》绝大多数的问题都是从其他数学著作如刘仕隆所著《九章通明算法》(公元1424元)和吴敬的《九章算法比类大全》(公元1450年)等书中摘取出来的。
纵观中国古代数学和数学类书籍的发展,可以看出,在《九章算术》的影响下,古代数学注重计算和实际问题的解决,轻视逻辑推理,所以古代数学算术发达而几何学不发达。而中国古代数学以解决实际问题为原则,遵循着构造性、算法化的思想,这与当今计算机算法思想不谋而合,随着现代计算机技术的快速发展,人们对算法的关注日益提升,中国古代数学构造性、机械化算法体系对今天的算法研究具有重要启迪作用。
此外,一些中国古代数学的经典理论与问题也经常出现在当今数学课本中,成为数学老师教案中必有的例题,例如《周髀算经》中的勾股术“折矩以为勾广三,股修四,径隅五”依然活跃在初中生的课堂上;《孙子算经》中的鸡兔同笼问题是二元一次方程的必考题型;南宋数学家杨辉在《详解九章算法》提出的“杨辉三角”多次成为奥林匹克数学竞赛试题等等。
名句千古颂,经典永流传。我国古代数学历史悠久、成就辉煌,那些流传下来的工具方法与理论著作是中华民族宝贵的智慧结晶。这些数学思想理论如今依旧散发着耀眼的光芒,为现代数学的发展贡献力量。